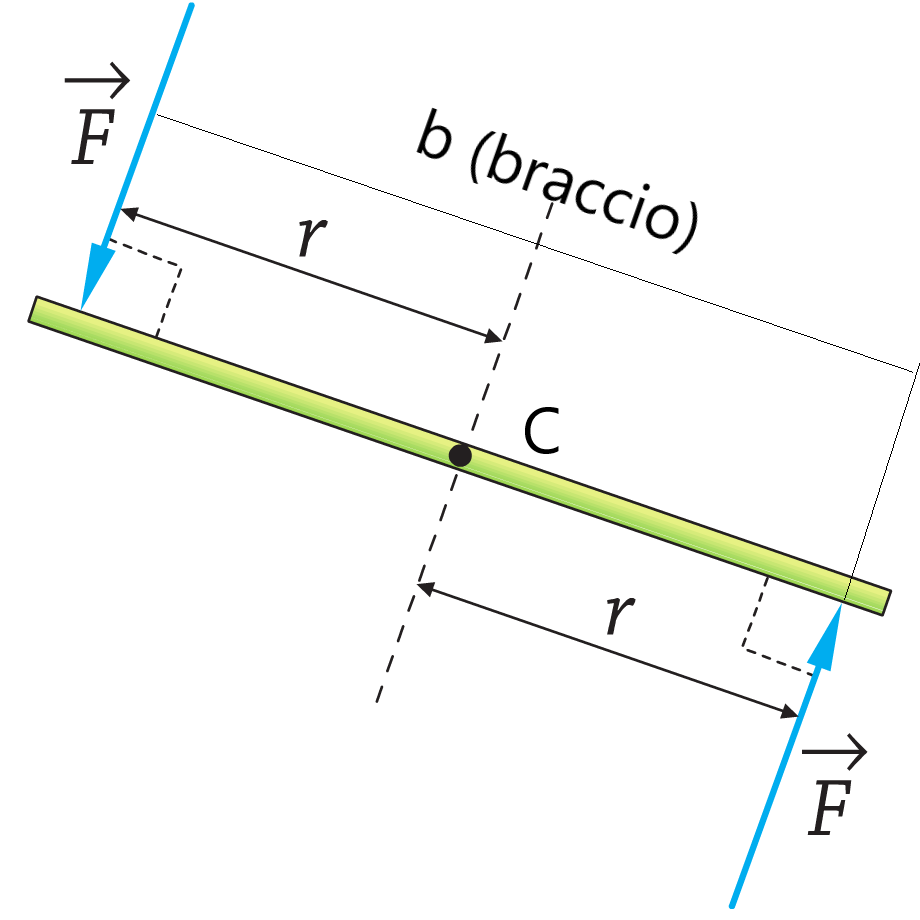
Il momento di una forza agisce mettendo in rotazione il corpo, ovvero variando la sua velocità angolare → varia la sua energia cinetica rotazionale, compiendo lavoro. Il teorema dell'energia cinetica → ΔK = Kf - Ki = ½ Iω2 f - ½ Iω2 i = L se il momento della forza è costante, il lavoro è L = τ(θ f - θ i). Soluzione: dalla figura osservo: la forza $F_1$ non produce momento poiché il suo braccio rispetto a C è zero, infatti la sua direzione passa per C; $F_2$ produrrà un momento antiorario (+) rispetto a C dato da: $M_ {2}=F_ {2}\cdot b_ {2}= 10\cdot 0,015=0,15 N\cdot m$ poiché il suo braccio $b_2$ è proprio la metà del lato del quadrato;

LA FISICA FACILE Il momento di una Forza YouTube

Massa e peso Prof. Filippo Brando

Momento di una forza ed equilibrio corpo rigido YouTube

PPT Unità 7 PowerPoint Presentation, free download ID3011581

PPT MECCANICA PowerPoint Presentation, free download ID5408326

Coppia di forze Prof. Filippo Brando

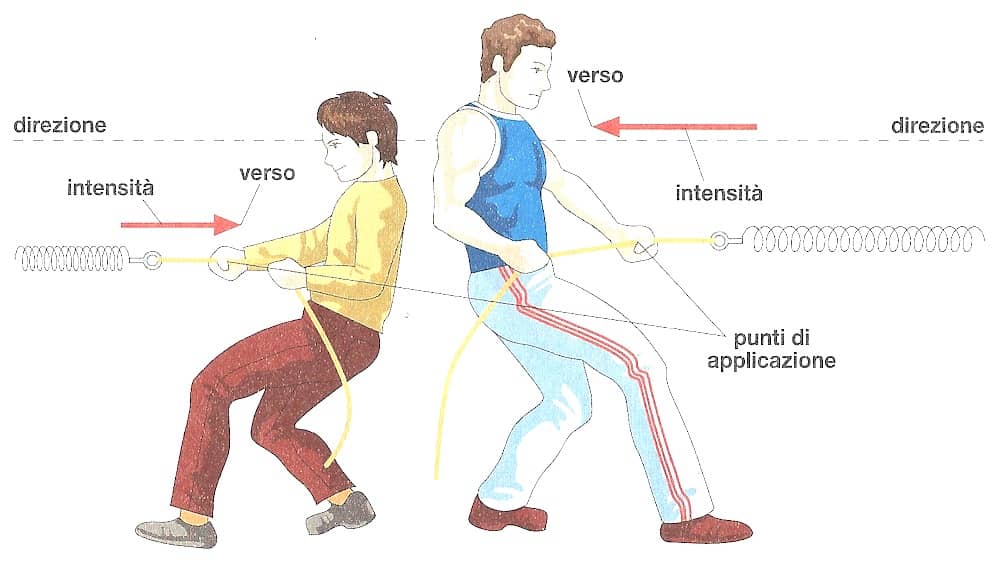
Forza in Fisica definizione, esempi, caratteristiche, misura Studia Rapido

Momento di una forza. YouTube

Obiettivo dell’esercitazione sperimentare il momento di una forza ppt scaricare

PPT Capitolo 4 Le forze PowerPoint Presentation, free download ID4580959

Momento di una forza rispetto ad un punto YouTube

PPT Unità 7 PowerPoint Presentation, free download ID3011581

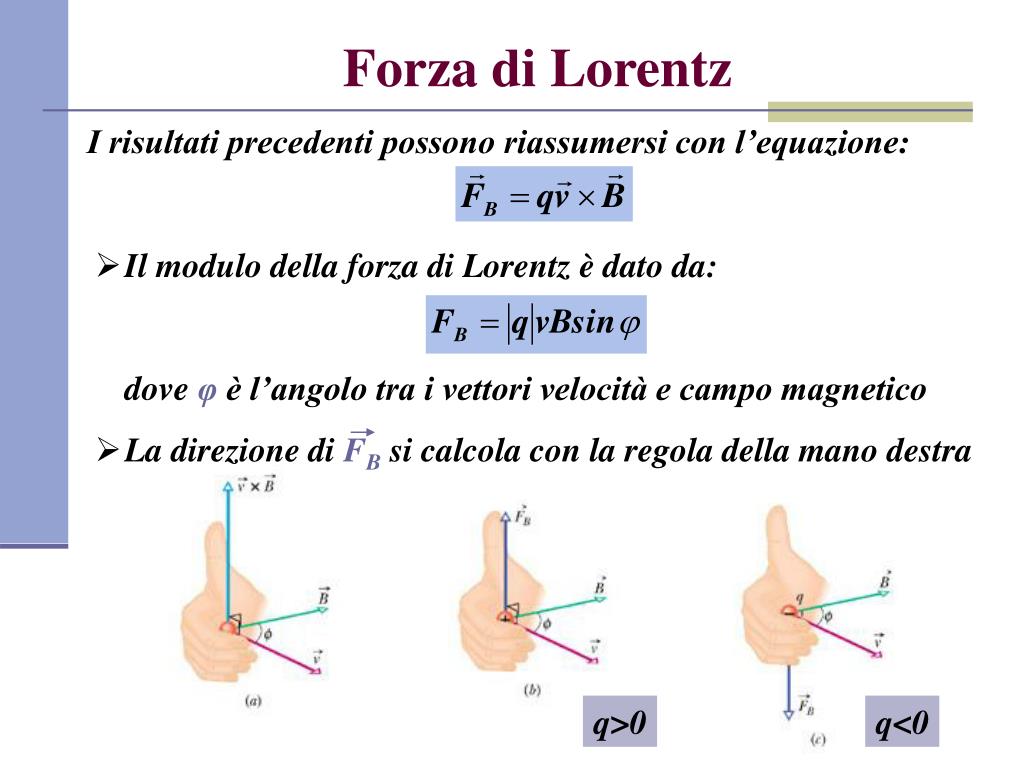
PPT Il campo PowerPoint Presentation, free download ID3922427

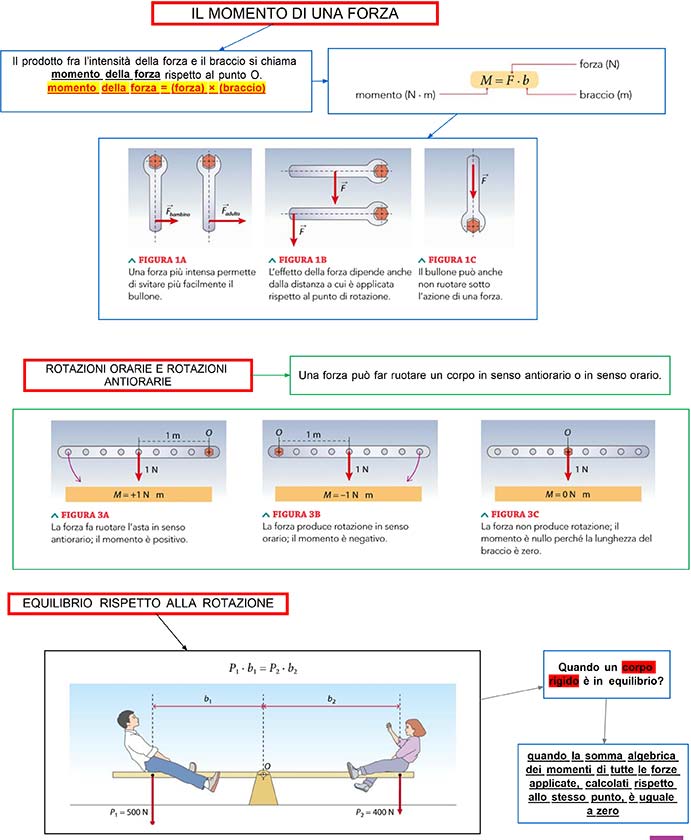
ilmomentodiunaforza DSA Study Maps

Momento di una forza il corpo rigido è in Equilibrio? YouTube

FISICA Momento di una forza YouTube

PPT Unità 9 PowerPoint Presentation, free download ID3011548

PPT Forze ed Equilibrio PowerPoint Presentation, free download ID2978924

PPT Unità 10 PowerPoint Presentation, free download ID3011569

Momento di una forza ESERCIZI YouTube

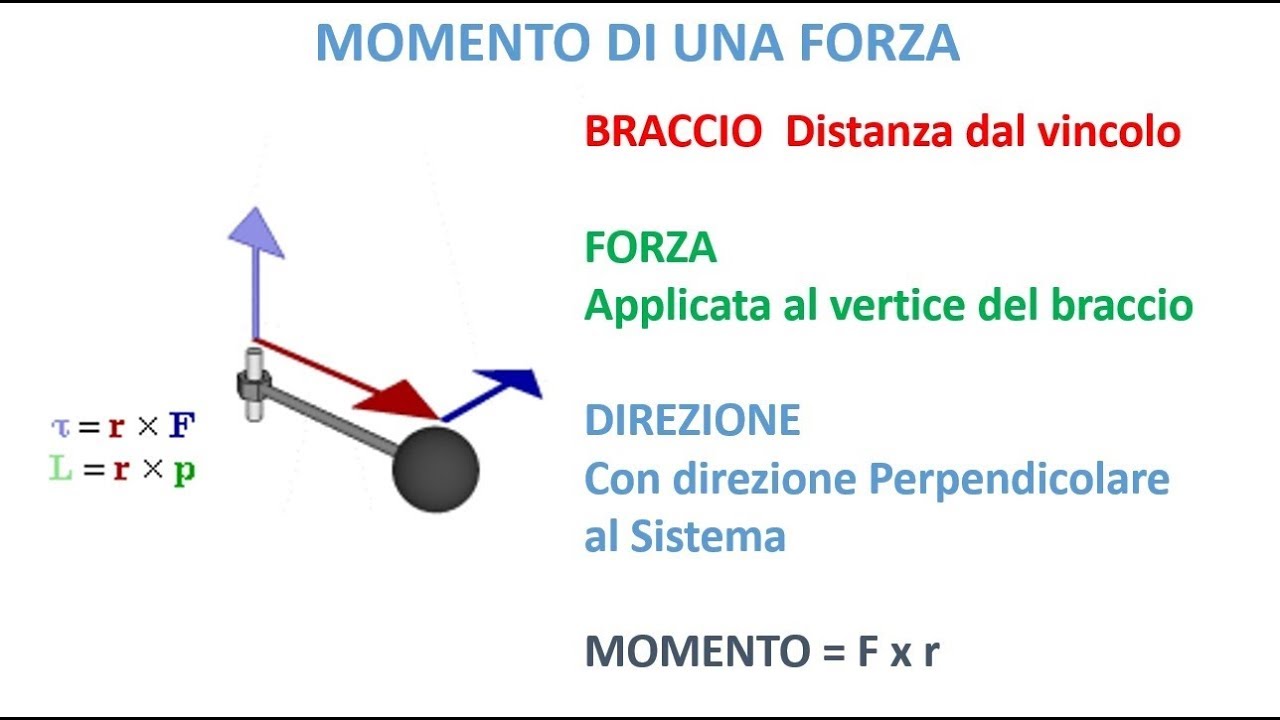
Aiuto compiti. Come si calcola il momento torcente. Cos'è e come si calcola il momento torcente: la guida con la formula e l'unità di misura per calcolare il momento di una.. Il momento di una forza è un vettore che esprime l'effetto di rotazione causato dalla forza stessa. In particolare, il vettore ha le seguenti caratteristiche: il suo modulo è dato dal prodotto dell'intensità della forza F e il modulo del braccio: M = F ∙ b; la sua unità di misura nel Sistema Internazionale è, quindi, Newton per metro ( N ∙ m );